LLGC

论文：Learning with Local and Global Consistency

LLGC 解读

参考 Wittawat Jitkrittum 解读

L: 靠近的数据点可能有相同的标签, 即 Local
G: 有相同结构的的数据点可能有相同的标签, 即 Global
C: 让每个点 iteratively spread 其标签信息到其临近, 直到实现全局稳定, 即 Consistency

1. Transduction

Input: ${x_i,y_i}{i=1}^{l}$ 和 ${x_i}{i=l+1}^{l+u}$
- $l \ll u$
- $n = l + u$
- $y_i \in {0,\cdots, C-1}$ (分类任务)
- 无需借助映射 $f: X \mapsto Y$, 便可推断 ${y_i}_{i=l+1}^{l+u}$
优势：比 Induction 更简单，因为无需映射 $f$, 仅仅做标签传播即可

2. Set Up

2.1 对于每个 $x_i$ 定义：

$Y_i := (\delta (y_i = 1),\cdots,\delta(y_i = C)) \in \{0,1\}^{1 \times C}$

若 $x_i$ 无标签比如, $i \geq l + 1$, 则 $Y_i = \mathbf{0}_{1 \times C}$.

2.2 对于每个 $x_i$, 通过 label propagation 来找到一个非负评分向量(nonnegative scoring vector) $F_i \in \mathbb{R}{+}^{1 \times C}$, 即 $F_i = (f{i1},\cdots,f_{iC})$.

2.3 目标: 通过固定的 $Y$ 来求得 $F$. 其中

$Y = \begin{pmatrix} Y_1\\ \vdots \\ Y_{l+u} \end{pmatrix}; F = \begin{pmatrix} F_1\\ \vdots \\ F_{l+u} \end{pmatrix}$

3 Label Propagation Algorithm

$W \in \mathbb{R}^{n \times n}$, 且 $W_{ii} = 0$.
标准化 $W$ 为

$S = D^{-\frac{1}{2}} W D^{-\frac{1}{2}}$

其中 $D$ 为对角矩阵, 且 $D_{ii} = \sum_{j}W_{ij}$.

迭代过程

$F(t + 1) \leftarrow \alpha SF(t) + (1 − \alpha)Y$

这里 $\alpha \in (0,1)$, 且 $F(0) = Y$

计算 $x_i$ 的标签

$y_i = \arg\max_k F^∗_{ik}$

这里 $F^∗ := \displaystyle\lim_{t \to \infty} F(t)$.

4 相似度矩阵

$\epsilon$-neighborhoods

$W_{ij} = 1 \text{ if } ||x_i − x_j|| < \epsilon$

May lead to several connected components.

$k$ nearest neighbors (kNN)

$W_{ij} = 1 \text{ if } x_i \in \text{ kNN}(x_j) \text{ or } x_j \in \text{ kNN}(x_i)$

Gaussian kernel:

$W_{ij} = \exp(− \frac{||x_i − x_j||^2}{2\sigma^2})$

5 注意事项

$W$ 捕获了数据的固有结构
设置 $W_{ij} = 0$ 以避免自我强化(self-reinforcement)
$\alpha$ 从近邻和 $Y$ 中权衡信息(High $\alpha \Rightarrow$ trust neighbors ($\alpha = 0.99$ in the paper))

$F(t + 1) \leftarrow \alpha SF(t) + (1 − \alpha)Y$

Analytic update(依赖于 $F(0)$)

$F^∗ = (1 − \alpha)(I_{n\times n} − \alpha S)^{−1} Y$

lgc

算法推导

原始数据由有标签数据 ${x_i,y_i}{i=1}^{l}$ 和无标签数据 ${x_i}{i=l+1}^{l+u}$ 组成. 其中

$x_i$ 可以是图片的像素级特征(一般分为灰度图和彩色图片)或者文本数据;
$y_i \in {0, \ldots, C-1}$ ($C$ 为 $x_i$ 所属类别的个数);
$l \ll u$

对于任意的特征 $x_i$, 通过特征提取器 $f$ 提取其语义特征向量为 $X_i = f(x_i)$, 且记

$X = \begin{pmatrix} X_1\\ \vdots \\ X_{l+u} \end{pmatrix}.$

下面便可以通过 $X_1,\ldots, X_n$ 来计算原始数据集的相似度矩阵 $W$, 记 $d_i = \sum_j (W)_{ij}$, 则有 $D = \text{diag}{d_1, \ldots, d_n}$ 和 $\Delta = D-W$. 为了利用向量化编程来提高算法的运算效率, 还需要将 $y_i$ 向量化:

$(Y_i)_j = \begin{cases} 1 & j = y_i \text{ and } i \leq l\\ 0 & 其他 \end{cases}$

这样, 便可定义

$Y = \begin{pmatrix} Y_1\\ \vdots \\ Y_{l+u} \end{pmatrix}.$

定义 $F \in \mathbb{R}^{n\times C}$ 满足

$y_i = \arg\max_j \; (F_i)_j$

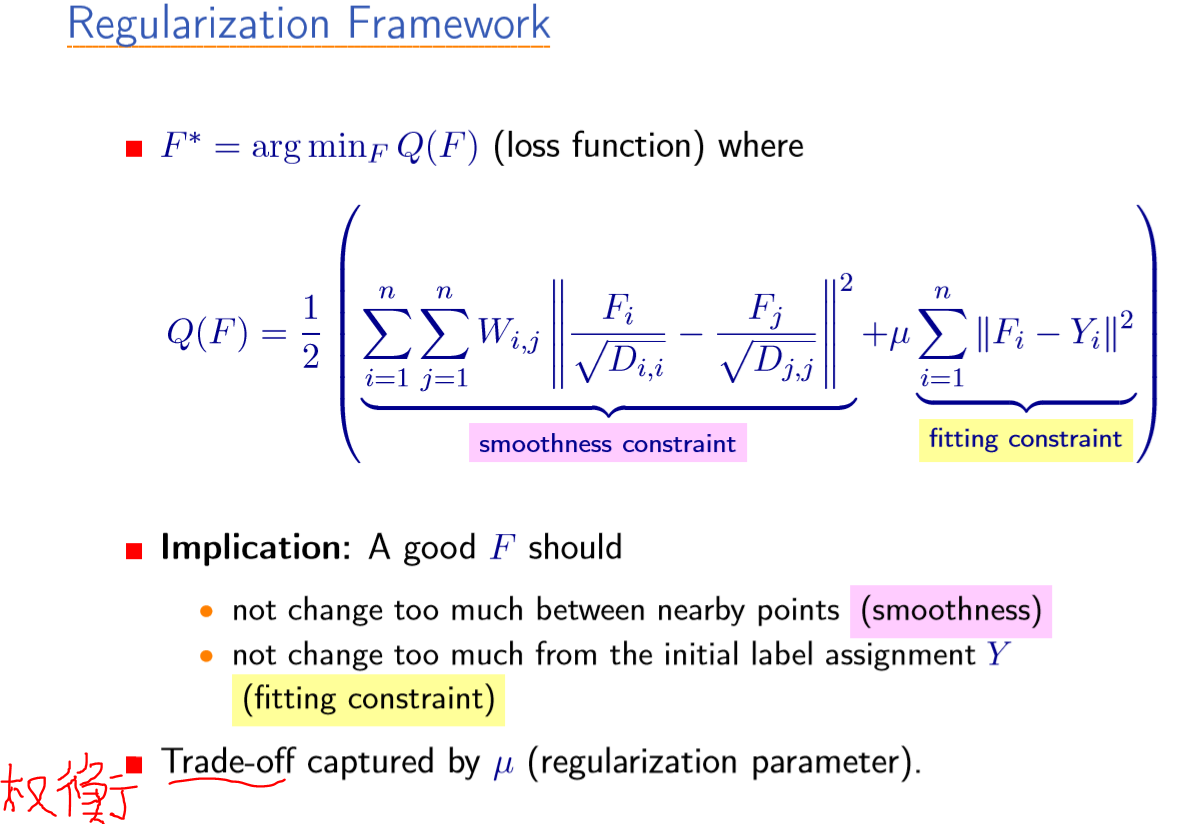
LGC 的目标是最小化能量函数

$\begin{aligned} Q(F) &= \frac{1}{2} {\displaystyle\sum_{i=1}^{n}\sum_{j=1}^n (W)_{ij} ||\frac{F_i}{\sqrt{(D)_{ii}}} - \frac{F_j}{\sqrt{(D)_{jj}}}||^2} + \mu \sum_i ||F_i-Y_i||^2\\ &= \text{tr} (F^T (I − S)F)+ \mu (\text{tr} (F^T F)− 2\text{tr}(F^TY)+ \text{tr}(Y^TY)) \end{aligned}$

其中 $\mu >0$ 用来权衡 L 与 G, 且

$S = D^{-\frac{1}{2}} W D^{-\frac{1}{2}}$

由 $\frac{\partial E(F)}{\partial F} = 0$, 可得 $(I − S)F + \mu (F − Y ) = 0$, 即可得迭代方程

$F(t+1)= \alpha SF(t) + (1-\alpha) Y$

其中 $\alpha = \frac{1}{\mu + 1}$. 故而 $0<\alpha<1$, 由 $F(0)=Y$, 可得

$F(t+1) = (\alpha S)^{t+1}Y + (1-\alpha) \sum_{i=0}^{t} (\alpha S)^i Y$

$t\to \infty$ 可得

$F^* = \beta (I-\alpha S)^{-1}Y$

$\beta=1$, 则表示非正则化的 LLGC, $\beta=1- \alpha$ 则表示正则化的 LLGC.

sklearn 算法实现 lgc

详细内容见：标签传播算法(llgc 或 lgc).

在 sklearn 实现中提供了两种不同 lgc 模型: LabelPropagation 和 LabelSpreading, 其中后者是前者的正则化形式. 相似度矩阵 $W$ 的计算方式提供了 rbf 与 knn.

rbf 核由参数 gamma控制（$\gamma=\frac{1}{2{\sigma}^2}$）
knn 核由参数 n_neighbors（近邻数）控制

DecodePaper

Interpreting and reproducing papers